A Little Useful Shop Math

by Richard McCandless

My son is a high school teacher. When I told him I'd used high school math to solve a common woodworking problem, he asked for an explanation. After all, he said, his subject is history!

He suggested I write a simple-English explanation of the math involved. He's sure lots of other people won't remember their school math any better than he, and I suspect he's right. So, with thanks to him, here is a useful math review.

On paper or in your head, draw a triangle where one angle is a right angle, that is, 90 degrees. This "right triangle" represents a common workshop problem. It can make your life easier. It can save material, time and frustration.

The problem is this: How do we find the length of an angled piece (call it "part C") that connects two pieces that, themselves, meet at a right angle (call them parts A and B)? You see this problem again and again.

Let's say you want a brace to back up the square corner of a cabinet or chair seat. How long will the brace be? You can cut wood, test it, cut and try again, until it fits or suddenly it's too short … but isn't that annoying?

Another example: You want an angled stringer to run diagonally across a new garden gate. Is the piece of expensive teak or cedar in your hand long enough? You can build the gate and then measure, but why not use a little math and know in advance?

Or, you plan to build a bridge over your pond. You want to buy timbers just the right length, but not to waste money buying them too long. You can throw measuring tapes back and forth (and into) the water, but the same math will give you the answer.

These problems are all alike. You can solve them all with a right triangle. Here's how. Go back to your drawing. It looks something like this:

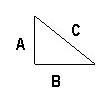
Notice that we've named the triangle's sides A, B and C, and the angle where A and B meet is 90 degrees, or a right angle (this is important). Again, this kind of triangle is called a right triangle.

Here's another important fact: It doesn't matter whether A and B are the same length or not. In other words, your triangle might look like any of these, and the math still works:

The man who worked out this math lived 2,500 years ago in Greece. His name was Pythagoras, and he's called "the father of numbers." Ol' Pythagoras found that for every right triangle the relationship between the sides A, B and C (where C is the diagonal side, the one opposite the right angle) is:

A² + B² = C²

In other words "A squared plus B squared equals C squared." Always. Does it matter whether the sides are in feet or inches, millimeters or miles? Nope. Just be sure you stick with the same units on all three sides, and you'll be fine.

Calculators do square roots automatically, so it's easy to use this formula (it's called the "Pythagorean Theorem") in any of our examples or any problem that vaguely resembles them.

How about an easy example? Take the garden gate I mentioned. You want to know the length of a diagonal stringer to go from one corner to the opposite corner. If your plan is for a gate that's three feet high and four feet wide, think of a triangle whose "A" is the bottom of the gate, "B" is one vertical side, and "C" is the diagonal line from one corner to the opposite one. You already know A and B, because one is 3 and the other is 4. Here's the math to find C:

A² + B² = C²

Plug in the measurements for A and B and we have:

3² + 4² = C²

Multiply 3 by itself and 4 by itself, and we have:

9 + 16 = C²

25 = C²

And what's the square root of 25? Ask the calculator if you aren't sure. It's 5. Corner to corner, the gate will measure exactly 5 feet. (Yes, yes, in real life a brace like this doesn't go corner to corner, but I made the first example easy.)

Here's a problem that looks different. Suppose your garden pond is an oval and you want a new bridge to angle across it, from a stake you've driven on one side to a stake on the other. Like me you have trouble walking on water. You can find the distance between the stakes without a miracle if you imagine a right triangle like this:

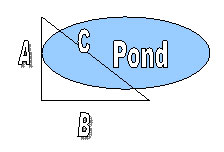
In this case "C" is where you want the bridge to cross the pond. You drive a stake in the ground so sides "A" and "B" are on land, where you can walk. As long as the angle between sides A and B is 90 degrees it doesn't matter where you put that third stake.

Now you can take measurements on solid ground. If A turns out to be 11 feet and B turns out to be 15 feet, put those numbers into the formula like this (I'll write each step):

A² + B² = C²

11² + 15² = C²

121 + 225 = C²

C² = 346

Use your calculator to take the square root of 346. It's 18.6. The bridge could be built on timbers 18.6 feet long.

It's surprising how often I use this formula. It's helped me buy wood, rope, electrical wire, and plumbing. It's a bit of geometry that's been useful for years.

A final point – this is important and sometimes it's not obvious. You can imagine and draw these triangles where you need them, so sometimes A and B and C are longer or shorter than whole length of the piece of wood, or whatever it is, underneath it. In the bridge-over-the-pond example, the triangle was bigger – side C is long enough so the timbers sit safely on shore, a foot or two away from the water. Many times sides A and B of your imaginary triangle will be shorter or longer than the entire workpiece. I often lay them out using even numbers, so I don't have to fiddle with fractions. Your triangle's corners may be "out in the air" somewhere. That's OK. All that matters is that side C be the length you want to measure.

You may find this little bit of math useful. A calculator makes it easy. And you can tell your friends you used your old trigonometry, and smile while they say "Wow!"